Unstructured vs. structured mesh occupancy

Hello all, this will be a quick post about how many cells it takes to fill a volume using unstructured cells and structured cells. This would presumably give some indication of how much computational work increases when using an unstructured mesh.

We will fill a simple cube of dimension 1 with cells of characteristic length 0.1, in gmsh (open source, free). I have included below the gmsh (.geo) script used to generate these meshes so that you may play around with the numbers. Here are is a visual comparison:

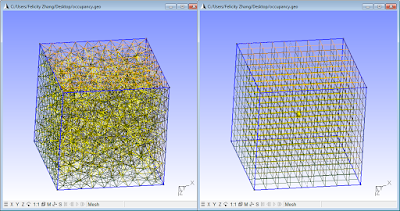
The results:

Unstructured: 1225 vertices, 6978 elements.

Structured: 1000 vertices, 1331 elements.

Meshing only the faces for a 2D comparison:

Unstructured: 593 vertices, 1297 elements.

Structured: 489 vertices, 603 elements.

So now I am a bit confused about vertices vs. elements. I would have thought 2D elements means 9*9*6 (9 for each dimension, 6 faces) = 486, which is darn close to the vertices count. Hmm if anyone knows please post, and if not in the meantime maybe I will get to updating this.

Interesting fact, I guess there may be some pseudorandomness in the mesh generation; reloading the file and remeshing gave slightly different results. Another element count I got for unstructured 3D meshing was 6624.

The script:

transfinite = 1;//toggle 0 or 1, for unstructured or structured, respectively.

cellLength = 0.1;

cubeLength = 1;



Point(1) = {0,0,0,cellLength};Point(2) = {0,0,cubeLength,cellLength};

Point(3) = {0,cubeLength,0,cellLength};Point(4) = {0,cubeLength,cubeLength,cellLength};

Point(5) = {cubeLength,0,0,cellLength};Point(6) = {cubeLength,0,cubeLength,cellLength};

Point(7) = {cubeLength,cubeLength,0,cellLength};Point(8) = {cubeLength,cubeLength,cubeLength,cellLength};

Point(9) = {0,0,0,cellLength};

Line(1) = {8, 7};

Line(2) = {7, 5};

Line(3) = {5, 6};

Line(4) = {6, 8};

Line(5) = {8, 4};

Line(6) = {4, 2};

Line(7) = {2, 6};

Line(8) = {3, 7};

Line(9) = {3, 4};

Line(10) = {3, 1};

Line(11) = {1, 2};

Line(12) = {1, 5};



Line Loop(13) = {5, -9, 8, -1};

Plane Surface(14) = {13};

Line Loop(15) = {10, 11, -6, -9};

Plane Surface(16) = {15};

Line Loop(17) = {7, 4, 5, 6};

Plane Surface(18) = {17};

Line Loop(19) = {3, 4, 1, 2};

Plane Surface(20) = {19};

Line Loop(21) = {8, 2, -12, -10};

Plane Surface(22) = {21};

Line Loop(23) = {3, -7, -11, 12};

Plane Surface(24) = {23};



Surface Loop(25) = {22, 14, 18, 24, 20, 16};

Volume(26) = {25};


If(transfinite==1)

Transfinite Line {1:12} = cubeLength/cellLength;

Transfinite Surface {14,16,18,20,22,24};

Recombine Surface{14,16,18,20,22,24};
Transfinite Volume {26};

EndIf