OpenFOAM 1.6-ext and GPU CFD

There has been some recent developments in application of GPUs (graphics processor units) for scientific computing. Only has the prominent CUDA language for programming for GPUs been released in 2006. GPU computing has been shown to offer an order of magnitude lower wall clock run times, at an order of magnitude of the price! It seems like the computing solution of the future for CFD at the very least! Its obstacle to widespread use has been in software implementation. But this is an obstacle that is fading away.

Here is a test case run by someone at the CFD-online forums:

http://www.cfd-online.com/Forums/openfoam-solving/99828-8x-icofoam-speed-up-cufflink-cuda-solver-library.html

So I was eager to buy a graphics card for $120 (GTX 550 Ti) and install OpenFOAM 1.6-ext, since Cufflink only works on 1.6-ext (I have been using 1.5-dev). There are quite a bit of differences, but it did not take me long to figure it out. The biggest difference is that 1.5-dev's GGI implementation uses PISO, and 1.6-ext uses PIMPLE. I could only get stability using smoothSolver for the turbulence quantities when using the kOmegaSST model (I only used smoothSolver in 1.5-dev as well because it was the only parallel-compatible solver I think, which may still be the case here...).

Looking forward to using the cutting-edge in software and computational power. Thanks to all the open source CUDA developers.

A note about GMSH scripting

This is about a frustrating detail that took me a few hours to discover. Scripting in GMSH allows one flexibility in design. The parameterization of the mesh allows for quick redesign. As objects can become complex rather quickly, when scripting in GMSH it may be helpful to make 'functions'. I say 'functions' because these are parameter-less and act as though you copy and pasted the function where you called it. So it is very primitive.

This caveat that took me some time to discover was that you have to be sure that calling a function is the last thing you do on a line, and do not have multiple calls in one line. Only after a line break does the program refresh the variables and such.

Unstructured vs. structured mesh occupancy

Hello all, this will be a quick post about how many cells it takes to fill a volume using unstructured cells and structured cells. This would presumably give some indication of how much computational work increases when using an unstructured mesh.

We will fill a simple cube of dimension 1 with cells of characteristic length 0.1, in gmsh (open source, free). I have included below the gmsh (.geo) script used to generate these meshes so that you may play around with the numbers. Here are is a visual comparison:

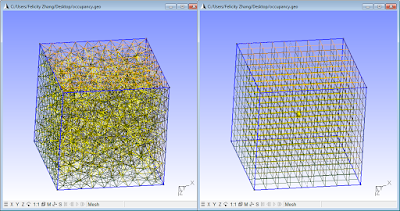
The results:

Unstructured: 1225 vertices, 6978 elements.

Structured: 1000 vertices, 1331 elements.

Meshing only the faces for a 2D comparison:

Unstructured: 593 vertices, 1297 elements.

Structured: 489 vertices, 603 elements.

So now I am a bit confused about vertices vs. elements. I would have thought 2D elements means 9*9*6 (9 for each dimension, 6 faces) = 486, which is darn close to the vertices count. Hmm if anyone knows please post, and if not in the meantime maybe I will get to updating this.

Interesting fact, I guess there may be some pseudorandomness in the mesh generation; reloading the file and remeshing gave slightly different results. Another element count I got for unstructured 3D meshing was 6624.

The script:

transfinite = 1;//toggle 0 or 1, for unstructured or structured, respectively.

cellLength = 0.1;

cubeLength = 1;



Point(1) = {0,0,0,cellLength};Point(2) = {0,0,cubeLength,cellLength};

Point(3) = {0,cubeLength,0,cellLength};Point(4) = {0,cubeLength,cubeLength,cellLength};

Point(5) = {cubeLength,0,0,cellLength};Point(6) = {cubeLength,0,cubeLength,cellLength};

Point(7) = {cubeLength,cubeLength,0,cellLength};Point(8) = {cubeLength,cubeLength,cubeLength,cellLength};

Point(9) = {0,0,0,cellLength};

Line(1) = {8, 7};

Line(2) = {7, 5};

Line(3) = {5, 6};

Line(4) = {6, 8};

Line(5) = {8, 4};

Line(6) = {4, 2};

Line(7) = {2, 6};

Line(8) = {3, 7};

Line(9) = {3, 4};

Line(10) = {3, 1};

Line(11) = {1, 2};

Line(12) = {1, 5};



Line Loop(13) = {5, -9, 8, -1};

Plane Surface(14) = {13};

Line Loop(15) = {10, 11, -6, -9};

Plane Surface(16) = {15};

Line Loop(17) = {7, 4, 5, 6};

Plane Surface(18) = {17};

Line Loop(19) = {3, 4, 1, 2};

Plane Surface(20) = {19};

Line Loop(21) = {8, 2, -12, -10};

Plane Surface(22) = {21};

Line Loop(23) = {3, -7, -11, 12};

Plane Surface(24) = {23};



Surface Loop(25) = {22, 14, 18, 24, 20, 16};

Volume(26) = {25};


If(transfinite==1)

Transfinite Line {1:12} = cubeLength/cellLength;

Transfinite Surface {14,16,18,20,22,24};

Recombine Surface{14,16,18,20,22,24};
Transfinite Volume {26};

EndIf