More omniwheel-drive control considerations

Here are some plots and MATLAB code that shows the relationship between the net contribution of the motors versus direction, for different numbers of motors/wheels on the vehicle. The 'net contribution' of the motors was calculated by adding the absolute value of the motor wheel direction (contribution direction) dotted with the direction of the vehicle's movement. The motor usage 'efficiency' is the same figure as described, but divided by the number of motors. An efficiency of 1 would be where all the motors are lined up and going the same direction, which will not happen with an omniwheel vehicle. The efficiency consistently floats around the .6-.7 range, which is pretty good. Meaning if I use 5 of these 135-watt DC motors, I would get about 440 W of rated DC power driving around. Not bad.

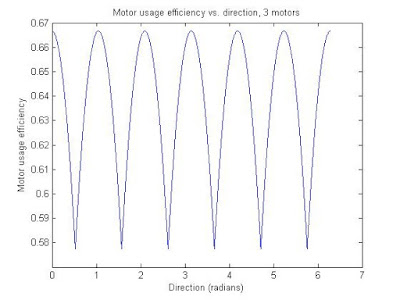
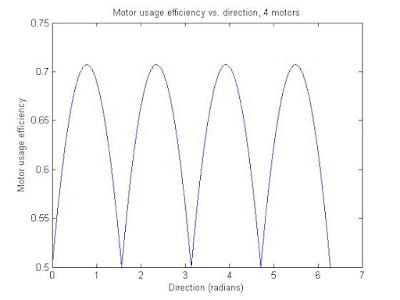
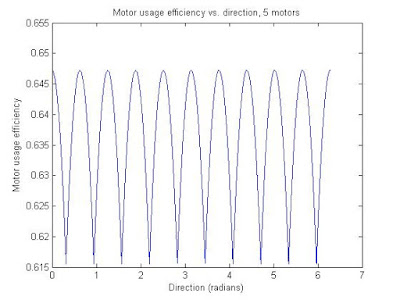
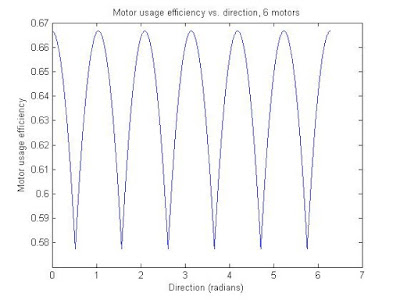
The code also includes last post's stuff (the speed consistency vs. direction plots). Again, even/odd wheel numbers are in their own trend groups, and as the number of motors go up the standard deviation of the efficiency with respect to direction goes down.

The efficiency plots:

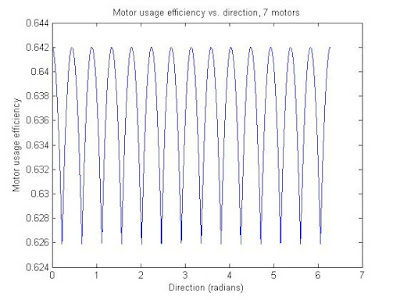
The code:

%FPS bot testing

close all;

offsetAngles = [0 0 0 0 0];%Just the difference in angle between frontmost motor and forward direction.

motorCounts = [3 4 5 6 7];

motorAngles = 2*pi./motorCounts;

for j = 1:numel(motorCounts)

mvec = zeros(motorCounts(j),2);

for k = 1:motorCounts(j)

mvec(k,:) = [cos(offsetAngles(j)+(k-1)*motorAngles(j)) -sin(offsetAngles(j)+(k-1)*motorAngles(j))];

end

resolution = 10000;

theta = linspace(0,2*pi,resolution)';

directionVector = zeros(resolution,2);

directionVector(:,1) = cos(theta);

directionVector(:,2) = sin(theta);

%Speed

mag = zeros(resolution,1);

currentMag = zeros(motorCounts(j),1);

for k=1:resolution

for i=1:motorCounts(j)

currentMag(i) = abs(mvec(i,:)*directionVector(k,:)');

end

mag(k) = max(currentMag);

end

figure;

plot(theta,mag);

ylabel('Normalized speed magnitude');

xlabel('Direction (radians)');

title(['Normalized speed magnitude vs. direction, ' num2str(motorCounts(j)) ' motors']);

%Torque

motorUse = zeros(resolution,1);

for k=1:resolution

for m=1:motorCounts(j)

motorUse(k) = motorUse(k)+abs(mvec(m,:)*directionVector(k,:)');

end

end

figure;

plot(theta,motorUse);

ylabel('Equivalent motor usage (# of motors)');

xlabel('Direction (radians)');

title(['Motor usage vs. direction, ' num2str(motorCounts(j)) ' motors']);

figure;

plot(theta,motorUse/motorCounts(j));

ylabel('Motor usage efficiency');

xlabel('Direction (radians)');

title(['Motor usage efficiency vs. direction, ' num2str(motorCounts(j)) ' motors']);

end